裏技的テクニックに頼る習慣がつくと危険
「プロ家庭教師をつけていたのにうまくいかない」という受験生を指導すると、よくその生徒から裏技的テクニックを求められることがよくあります。前の先生はそれを教えてくれたというのです。
難しい理屈ではなく、それを適用しただけでパパパと正解が取れてしまうテクニックが確かに存在します。そのようなものは、「裏ワザ」「裏技的テクニック」と言われます。例えば次のようなものです。
ラグビーボールの公式
以下のように、四分円を正方形になるように2つ重ねたときにできる、中央のラグビーボールのような形の面積は、ある裏技的テクニックですぐに正解が出せます。
以下の図形の正方形の中にある斜線の面積を求めなさい。円周率は3.14とする。
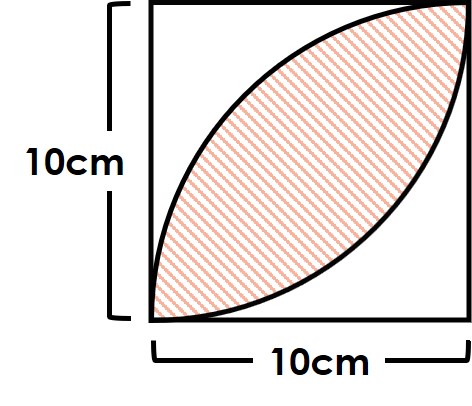
解き方は簡単です。10×10×0.57=57(cm2)これだけ。このやり方をよく「ラグビーボールの公式」とか「ラグビーボールの法則」と言われます。
つまり正方形に0.57倍をすれば正解が取れるのです。ただ適用するだけでいいので、すごく楽に正解が取れます。
そこでこういうテクニックで味をしめた受験生は「他にこういうただ数字を入れるだけで解けるテクニックはないのか?」と求めてくるわけです。
しかしこのような裏技的テクニックは非常に危険です!
ラグビーボールの公式の危険な点
実はラグビーボールの公式を使わなくても、この問題は簡単で、たいていの受験生は本来のやり方で取れるのです。そのように考えると、間違えることは許されない。万一間違えたら致命傷になる問題といえます。
これに対して、ラグビーボールの公式は以下のようなミスの可能性が内包します。
円周率が3.14のときでないと間違える
ラグビーボールの公式は、円周率が3.14を前提として成立するテクニックです。これを押さえていない受験生が結構います。円周率を3.14以外にして出題されたら一巻の終わりです。
数字が曖昧になると間違える
このラグビーボールの公式が使える局面は非常に珍しいため、受験生の立場で言えば不意打ち的に出題されます。このとき、一見無味乾燥な0.57が思い出せるかどうかですが、記憶が曖昧であることが多いです。0.53などで計算したり、掛けないで割ってしまったり。
そもそもがこの問題は正答率が高いので、このようなつまらないミスが起きる危険性を考えれば、私はあまり教えたくないのです。しかし算数指導者には、鬼の首を取ったかのようにこのテクニックを教えたがる人が多いことは知っています。入試の合否のことを考えると、私には理解できません。
少なくとも私はこのラグビーボールの公式を、算数弱者には教えません。教えてもある程度レベルに達している受験生に、しかもあくまで検算か参考程度に教えます。
また、こういう裏技的テクニックには、これ以上に危険な側面があります。
一番大きな危険:裏技的テクニックに頼る癖がつくと、裏づけを取って学ばなくなる!
裏技的テクニックに頼る癖がつくと、算数のどの分野に対しても裏づけを取って学ばなくなる傾向にあります。私の指導経験では、こういう生徒が一番苦労します。表面的なテクニックの楽さに味を占めて、算数の本質から目を背けることをしてしまうのです。
したがって裏技的テクニックは、よほど汎用性の認められるものでない限り、私の中では利点を打ち消して有り余るほど有害と考えてしまいます!これなら、学ばない方がよほど合格には近いと考えます。
その問題につき鮮やかに解答できても、算数全体がだめならお話しにならないのです。
このような多くの指導者が前面に出して教えたがる「裏技的テクニック」は注意したほうが良いと思います。その瞬間楽だからといって、決して深入りしてはいけないものです。
算数を学ぶ際は非常に注意していただきたいと思います。